You are here
Systems of Equations - Research and Practice Guide
Introduction
Systems of equations (or "simultaneous equations") involve the solving of two or more equations containing two or more unknowns.
Understanding the Challenge
What Makes Systems of Equations Difficult for Teachers?
The aspects of systems of equations that are challenging to students adds to the challenge of teaching them. However, teachers have an additional complication of figuring out a curricular progression to support students' learning. In a very basic (read: not standards-aligned) math textbook, you may only see three steps in the progression: (1) graph lines and find the point of intersection, (2) solve using the substitution method, and (3) solve with the elimination method.
If we look to the standards, as with most other topics, we can expect to find a progression of learning that builds procedural fluency with conceptual understanding. Systems of equations first appear in Grade 8:
8.EE.C.8. Analyze and solve pairs of simultaneous linear equations.
8.EE.C.8.a. Explain that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.
8.EE.C.8.b. Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6.
Interpreting these 8th grade standards presents some challenges. The evidence outcome asks that students "analyze and solve," and limits the systems to linear equations. Part (a) of the evidence outcome addresses the conceptual understanding of what it means to be a solution to a system of equations, and Part (b) provides details about the procedural aspect of solving them. This is where interpreting the standards gets unclear. If we piece together the language in Part (b), it does say "solve ... algebraically," which some might interpret as solving using the substitution and elimination methods, which are the formal, abstract approaches expected near the end of a learning progression. However, Part (b) also says students should "estimate solutions by graphing" and "solve simple cases by inspection," both of which are less formal methods a person would expect earlier in a learning progression. The standards for 8th grade do not mention substitution and elimination, and it isn't clear that they should be part of the 8th grade curriculum.
Systems of equations also appear in the high school standards:
HS.A-REI.C.5. Prove that, given a system of two equations in two variables, replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions.
HS.A-REI.C.6. Solve systems of linear equations exactly and approximately (e.g., with graphs), focusing on pairs of linear equations in two variables.
HS.A-REI.C.7. Solve a simple system consisting of a linear equation and a quadratic equation in two variables algebraically and graphically. For example, find the points of intersection between the line y = −3x and the circle x2 + y2 = 3.
Again, there are no explicit mentions of the substitution and elimination methods, but careful interpretations can provide some guidance here. HS.A-REI.C.5 is essentially describing the elimination method, not for students to solve with it, but to prove that the method works. (See the lone A-REI.C.5 Illustrative Mathematics task for an example and an explanation.) HS.A-REI.C.6 directs students to solve systems of linear equations exactly and approximately. The language here is very similar to part of 8.EE.C.8.b, but more direct and unambiguous. HS.A-REI.C.7 also asks students to solve systems of equations, but to include non-linear equations.
So if the 8th-to-high school progression of learning systems of equations starts with the conceptual understanding of what a solution to a system of equations represents, and finishes with procedural fluency of solving systems involving both linear and non-linear equations, what does the middle of that progression look like? The standards describe some of the building blocks but don't say enough to really help teachers and curriculum designers to see all the curricular possibilities.
Recommendations
Focus on Two of NCTM's Effective Teaching Practices
Two of NCTM's Effective Teaching Practices are especially relevant when teaching systems of equations: (#3) Use and connect mathematical representations and (#6) build procedural fluency from conceptual understanding.
3. Use and connect mathematical representations. Teachers commonly think of multiple representations as equations, tables, and graphs. But if you look more carefully at this practice in Principles to Actions (NCTM, 2014, p. 25), the types of representations discussed there are contextual, physical, symbolic, verbal, and visual. This effective teaching practice calls on teachers to introduce forms of representations that can be useful to students and to focus students' attention on the structure or essential features of the mathematical ideas that appear, regardless of the representation. While this can and should be done with equations, tables, and graphs, there's a far broader set of representations and models that can be useful when learning about systems of equations.
6. Build procedural fluency from conceptual understanding. The formal procedures of solving systems of equations using the substitution and elimination methods should be built on a foundation of conceptual understanding that may take months or even years to build. This conceptual understanding should include the use of informal reasoning strategies that teachers can help students connect to the meanings and properties of more formal operations, such as substitution and elimination.
Together, these two practices set the stage for building a curricular progression for the learning of systems of equations.
Introduce and Reason with Informal, Contextual Situations to Build Understanding
The idea that mathematics learning should be rooted first in contextual, informal situations is common in numerous theories, programs, and curricular materials, but is probably most strongly connected with Realistic Mathematics Education, a theory and approach born in the Netherlands in the late 1960s and 1970s, and still evolving today (van den Heuvel-Panhuizen & Wijers, 2005). One curricular resource that adopted this approach for the United States was Mathematics in Context, a grades 5-8 series of units that included one unit, "Comparing Quantities" (Kindt, Abels, Dekker, Meyer, Pligge, & Burrill, 2006) that focused on the use of informal contexts and "pre-formal" representations and models to develop conceptual understanding of systems of equations. The example tasks below all come from this unit, which is no longer in print.
Tug-of-War

Tug-of-War. © Encyclopædia Britannica.
The "tug-of-war" task asks students to reason through two known equal conditions (four oxen = five horses and one elephant = an ox and two horses) and use that knowledge to answer the question, "Which animals will win the tug-of-war below?" where an elephant and three horses are pulling against four oxen.
Students, even those in 6th grade or below, can reason with tasks like this without the use of any mathematical symbols or formal procedures. They will likely come up with the following approaches:
- Substituting the elephant on the left for an ox and two horses gives us five horses and an ox pulling against four oxen. Then substituting the four oxen on the right for five horses gives us five horses and an ox pulling against five horses. Because both sides have an equal number of horses, the left side will win the tug-of-war because it is also pulling with an ox.
- Substituting the elephant on the left for an ox and two horses gives us five horses and an ox pulling against four oxen. If we remove the ox from the left and one of the oxen from the right, which should pull equally, that gives us five horses pulling against three oxen. Since we know that five horses pull the same as four oxen, we know the left side will win the tug-of-war because the right side only has three oxen.
- Substituting the four oxen on the right side with five horses gives us an elephant and three horses pulling against five horses. If we remove three horses from the left and three horses from the right, which should pull equally, that gives us one elephant pulling against two horses. Since we know that an elephant pulls the same as an ox and two horses, the left side will win the tug-of-war because the right side only has two horses and no ox.
The tug-of-war task not only presents students with a context that could be real in the students' minds, but it also presents the concept of equality as relational, rather than operational, which can be a significant stumbling block for students. Balance representations (like a balance for finding the mass of objects, with a pan or tray on the left balanced with one on the right) also reinforce a relational conception of equality. Without introducing formal symbolic representations, teachers can help students with these types of tasks by focusing on the act of substituting and pressing students to explain their reasoning of what can be substituted for what and why.
Umbrellas and Caps

Umbrellas and Caps. © Encyclopædia Britannica.
Another type of task to build conceptual understanding of systems of equations are "combination" tasks. These could be combinations of lengths and widths, heights and weights, or combinations of products totaling a price. The "Umbrellas and Caps" task from Mathematics in Context is one such task, where students are given the knowledge that two umbrellas and a cap are worth $80, while one umbrella and two caps are worth $76. The question students should want to answer becomes, "How much does one umbrella cost? How much does one hat cost?" Just as with Tug-of-War, students can reason through this task without the introduction of formal mathematical symbols and representations. Solution strategies may include:
- Comparing the two combinations to conclude that an umbrella is $4 more than a hat, then guessing and checking with different prices until they find prices that work in both combinations.
- Adding the first combination to the second to give three umbrellas and three hats for $156, then reasoning that one umbrella and one hat must cost $52. Combined with the understanding that an umbrella is $4 more than a hat, an umbrella must be $28 while a hat is $24.
- Seeing a pattern from the first combination to the second that involves removing an umbrella, adding a hat, and subtracting $4. If the pattern is followed to a third combination, that combination would have three hats at a cost of $72, which means each hat is $24. Similarly, if the pattern is followed in the reverse direction, a new combination shown on top would have three umbrellas for $84, which means each umbrella is $28.

Candles. © Encyclopædia Britannica.
These price combination tasks engage students in contexts that are real to them and can be reasoned with. Tasks like the candles task are written to engage students directly in the reasoning of another student. Whereas the tug-of-war task built conceptual understanding for the substitution method, these price combination tasks open up more opportunities to develop a conceptual understanding for the elimination method, as well as the idea that "equals added to equals are equal" and "equals subtracted from equals are equal," which happen to be Common Notions #2 and #3 from Euclid's Elements, Book I.
Engage Students in the Use of Pre-Formal Models and Representations
One of the primary features of Realistic Mathematics Education are the concepts of progressive formalization and emergent modeling. Progressive formalization (Webb, Boswinkel, Dekker, 2008) is the idea that students should begin learning with informal, contextual representations, then move to "pre-formal" representations and models that help bridge conceptual understanding towards procedural fluency, then finally to formal mathematics, which is usually symbolic and dependent on procedural fluency. Emergent modeling (Gravemeijer, 1997) is the idea that the models students initially use are models of the informal context, but as their reasoning and use of the model becomes more sophisticated, they become models for reasoning with a generalizable mathematical idea. While this is similar to concrete-representational-abstract (CRA) perspectives on progressions of student learning, they are not quite the same. CRA implies that learning should start with the concrete, but if that "concrete" manipulative is something like Algebra Tiles, which are physical manipulatives, students may not have enough understanding of the tiles or context for their use to make them "real" in their minds. With progressive formalization and emergent modeling, the informal context comes first, and then "concrete" representations may be introduced to reason with the context.
Combination Charts and Notebook Notation
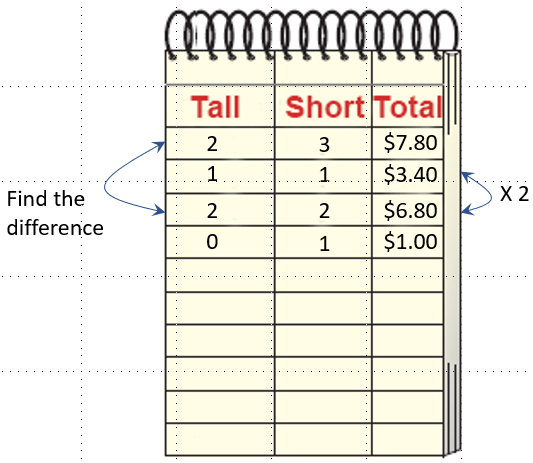
Notebook Notation. © Encyclopædia Britannica.
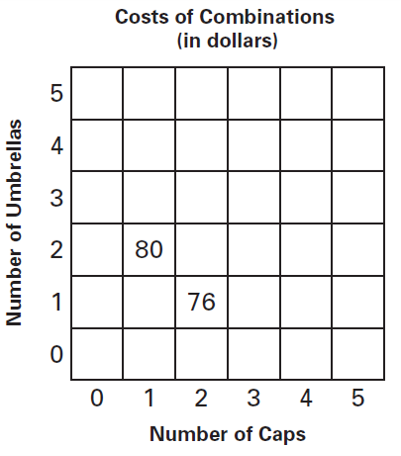
Combination Chart. © Encyclopædia Britannica.
Pre-formal representations of systems of equations include representations such as combination charts and notebook notation. The combination chart shown here matches the umbrellas and caps task, with the number of caps displayed along the horizontal axis and the number of umbrellas displayed along the vertical axis. This placement of two variables in two dimensions can help students connect their understandings of systems in two variables to graphing in the coordinate plane. Students should work to fill in the combination chart and to recognize and explain patterns they find. For example, each diagonal move down and to the right reduces the price by $4, and represents taking away one umbrella and adding one cap. Each diagonal move up and to the right adds an umbrella and a cap and increases the price by $52. These two diagonal moves on the combination chart match the actions of subtracting and adding the two combinations together. These diagonal moves can be continued until students are on the left or bottom edges, at which point they are counting only umbrellas or only caps and can find the per-unit price. This can be connected to the need to reduce the a systems of equations problem to one of the variables so that it can be solved for.
Notebook notation is another pre-formal representation. The notebook notation shown here matches the candles task and uses columns to organize the number of tall candles, the number of short candles, and the cost of each combination. One advantage of notebook notation is that it can easily accommodate more than two variables, which is a limitation of combination charts. Notebook notation encourages students to perform operations on a row, such as multiplying a row by 2 to make a new row (double the candles, double the cost) or to subtract one row from another to "eliminate" one of the variables (like the subtraction of Row 3 from Row 1 in this example, which eliminates the tall candles). Another advantage of notebook notation is that the work is organized vertically, much like work is shown when solving systems of equations algebraically, and students can annotate each new row with explanations of the operations they used to calculate it.
Plan for a Multi-Year Progression for Learning Systems of Equations
While the progression of learning systems of equations described by the standards is unclear, especially in which algebraic methods are to be introduced and mastered and when, it is clear that the progression should span over multiple years. In addition, the Effective Teaching Practices remind us to use and connect mathematical representations and to build procedural fluency from conceptual understanding. Together, these recommendations strongly suggest that the formal, generalized methods of substitution and elimination should not be expected of 8th grade students.
For 8th grade students, it is recommended to begin with informal contexts and then connect those to pre-formal representations. To meet the requirements of 8.EE.C.8, some contexts should lend themselves to being easily represented as tables and graphs, as those representations can also be used to develop understanding along with other pre-formal representations like combination charts and notebook notation. For solving simple cases by inspection, presenting these informally will likely make them easier to understand at first. For example, two shirts and two hats priced at $100 and the same two shirts and two hats priced at $90 indicates no solution because two shirts and two hats cannot simultaneously be two different prices. This kind of reasoning can be extended to the "simple cases" asked for in 8.EE.C.8.b in the form of the system 2S + 2H = 100 and 2S + 2H = 90.
For high school students, it is recommended to continue using informal contexts to aid with student reasoning, and to build strong connections between pre-formal models and formal representations and methods. Even once students are well-practiced with the formal methods of substitution and elimination, they may still find pre-formal models useful. One example of this will be when they are asked to solve systems involving non-linear functions, as asked for in HS.A-REI.C.7.
References
Alibali, M. W., Knuth, E. J., Hattikudur, S., McNeil, N. M., & Stephens, A. C. (2007). A longitudinal examination of middle school students’ understanding of the equal sign and equivalent equations. Mathematical Thinking and Learning, 9(3), 221–247. https://doi.org/10.1080/10986060701360902
Gravemeijer, K. (1997). Solving word problems: A case of modelling? Learning and Instruction, 7(4), 389–397. https://doi.org/10.1016/S0959-4752(97)00011-X
Kindt, M., Abels, M., Dekker, T., Meyer, M. R., Pligge, M. A., & Burrill, G. (2006). Comparing quantities. In Wisconsin Center for Education Research & Freudenthal Institute (Eds.), Mathematics in Context (2nd ed., p. 49). Encyclopædia Britannica.
NCTM. (2014). Principles to actions: Ensuring mathematical success for all. National Council of Teachers of Mathematics.
van den Heuvel-Panhuizen, M., & Wijers, M. (2005). Mathematics standards and curricula in the Netherlands. ZDM, 37(4), 287–307. https://doi.org/10.1007/BF02655816
van Reeuwijk, M. (2001). From informal to formal, progressive formalization an example on “solving systems of equations.” In H. Chick, K. Stacey, J. Vincent, & J. Vincent (Eds.), The future of teaching and learning of algebra: The 12th ICMI study conference (pp. 613–620). http://repository.unimelb.edu.au/10187/2812
Webb, D. C., Boswinkel, N., & Dekker, T. (2008). Beneath the tip of the iceberg: Using representations to support student understanding. Mathematics Teaching in the Middle School, 14(2), 110–113. https://doi.org/10.5951/MTMS.14.2.0110


Connect With Us





